안녕하세요. 이번 시간은 삼각함수에 대해서 알아보도록 합시다.
우선 삼각함수를 알려면 cos, sin, tan가 어떻게 정의되는지부터 알아봐야겠죠?

위와 같이 직각 삼각형의 변의 길이를 각각 A,B,C라고 하고 A,B 사이에 끼인 각을 x라고 한다면,
sinx=C/A
cosx=B/A
tanx=C/B
로 정의합니다.
사인, 코사인, 탄젠트를 정의하는 방법은 위의 방법 뿐만 아니라 단위원을 통해서도 정의를 합니다. (다음 그림에서는 r로 나와있지만, r=1인 원을 단위원이라 하므로 r=1이라고 생각하시면 되겠습니다.)
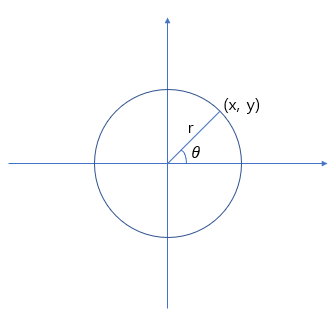
sinθ=y/1
cosθ=x/1
tanθ=y/x=sinθ/cosθ (tanθ는 x,cosθ≠0인 곳에서만 정의된다.)
와 같이 정의합니다.
반대로 x=rcosθ, y=rsinθ, 직선의 기울기는 tanθ임을 알 수 있습니다. 단위원이 아닌 경우에 대해서 생각해보시면, 바로 이해가 되실겁니다.
공부하시다가 혹시라도 둔각에서는 어떻게 정의된거지라고 생각하셨다면, 2번째의 정의를 따랐기 때문이라고 생각하면 되겠습니다.



그림으로 나타내면, 위와 같이 y=sinx, y=cosx, y=tanx로 나타나겠습니다.
자 그림을 보면서 삼각함수의 성질을 설명드리겠습니다.
우선 sinx와 cosx는 2π를 주기로 갖는 주기함수로 다음과 같이 증감합니다.
| 0 | π/2 | π | 3π/2 | 2π | |
| sinx | 0 | 1 | 0 | -1 | 0 |
| cosx | 1 | 0 | -1 | 0 | 1 |
tanx는 cosx≠0인 정의역을 갖습니다. 따라서 tanx의 정의역은 x≠{(2n+1)/2}π인 모든 실수로 정의됩니다. (n은 정수)
그래서 그림을 잘 보면, 그림에 점근선이 여러개인 그래프가 보이게 되죠.
사인, 코사인, 탄젠트는 특정 각에서의 값들이 자주 사용되는데, 이 값들은 외워두도록 합시다. (사실 삼각함수에서는 외워둘 것들이 은근 있기 때문에, 개념서 등을 이용해 모두 잘 외워두고 넘어갑시다.)
| 0 | π/6 | π/4 | π/3 | π/2 | |
| sinx | 0 | 1/2 | √2/2 | √3/2 | 1 |
| cosx | 1 | √3/2 | √2/2 | 1/2 | 0 |
| tanx | 0 | 1/√3 | 1 | √3 | ∞ |
삼각함수는 다음과 같이 다양한 형태로 변형될 수 있습니다.
| sin(-x)=-sinx | cos(-x)=cosx | tan(-x)=-tanx |
| sin(x+π/2)=cosx | sin(x+π)=-sinx | sin(x+3π/2)=-cosx |
| cos(x+π/2)=-sinx | cos(x+π)=-cosx | cos(x+3π/2)=sinx |
| tan(x+π/2)=-cotx | tan(x+π)=tanx | tan(x+3π/2)=-cotx |
우선 첫 번째 줄같은 경우는 그래프를 보면 사인과 탄젠트는 기함수라는 사실을 알 수 있고, 코사인은 우함수라는 사실을 알 수 있습니다. (cot는 탄젠트의 역수로 밑에서 다시 다루도록 하겠습니다.)
함수
함수의 정의는 '어떤 집합 X에서 어떤 집합 Y로의 대응'으로 정의됩니다. 기호로는 로 정의합니다. 'X를 f의 정의역, Y를 공역이라고 부르며, f(x)를 f에 의한 x의 상이라고 부르며, 그러한 상의 집합
gonbuine.tistory.com
밑에는 다음 예제를 통해 한 번에 이해해버리도록 합시다.
단위원이 그려진 다음 그림을 이용해 sin(θ+π/2)=cosx임을 보여라

해설: 위의 원은 단위원이기 때문에 각 θ인 직선과 원의 교점은 (cosθ, sinθ)이다. 이 점을 a라고 하자.
그리고 직선을 90도를 돌려주면 원과의 교점 (cos(θ+π/2), sin(θ+π/2))이 나온다. 이 점은 b라고 하자.
또한 이 점은 다음과 같이 쓸 수 있다. (-sinθ, cosθ)
여기서 sin에 -가 붙는 이유가 헷갈린다면, y가 x축인 좌표계를 그려보자. 그러면 우선 x가 음이고 y가 양이기 때문에 x/1=-sinθ가 되게 된다. 따라서 (cos(θ+π/2), sin(θ+π/2))=(-sinθ, cosθ)이다.
이와 같은 방법으로 표에 있는 나머지 변형된 형태들도 이해하시면 되겠습니다.
다음으로는 삼각함수의 합차공식과 배각 공식에 대해 알려드리려 합니다. 증명은 다음 시간에 따로 올리도록 하겠습니다.
삼각함수 덧셈정리 증명
안녕하세요. 오늘은 삼각함수 덧셈정리에 대해 증명을 해드리려고 합니다. 개인적으로는 한 번쯤은 이 부분에 대해서 찾아보거나 하는 걸 추천드리긴 하지만, 이 부분은 증명하는법을 계속해서
gonbuine.tistory.com
합차공식



배각 공식


우선 저같은 경우에는 합차공식을 외울 때 사인함수는 싸코코싸, 코사인함수는 코코싸싸, 탄젠트는 그냥 외웠던 것 같은데요. 도움이 되셨기를.. ㅋㅋ
마지막으로 삼각함수의 역함수에 대해서 배워봅시다.
2020/11/16 - [미분적분학] - 함수-함수의 결합, 역함수
함수-함수의 결합, 역함수
이번 시간은 함수의 결합과 역함수에 대해서 배워보도록 하겠습니다. 이번 시간에는 함수를 결합하는 방법을 크게 두 가지만 배워갑시다. 첫 번째로는 사칙연산을 통한 함수의 결합입니다. 사
gonbuine.tistory.com
우선 역함수에 대해서 잘 모르신다면, 밑에 역함수 파트만 잠시 읽고 오시면 될 것 같습니다.
우선 역함수를 만들때에는 일대일 대응인 함수만을 역함수로 만든다고 했었습니다. 삼각함수는 우선 세 함수 모두 일대일 대응함수가 아닙니다. 왜냐면 여러 정의역이 하나의 치역에 해당하는 경우가 많기 때문입니다.(ex. sin(0),sin(π)=0)
그래서 삼각함수의 역함수는 공역과 정의역을 조정해서 삼각함수의 역함수를 만들겁니다.
이런걸 왜 하나 싶겠지만, 수학을 오래 공부하면 자주 사용되는 함수이기 때문에 알아두면 좋습니다.
그렇다면, 사인함수 먼저 보도록 해보겠습니다.
사인함수의 치역은 우선 -1~1입니다. 그렇기 때문에 공역을 [-1,1]로 해줍니다.
그 다음 사인함수는 단사함수가 아니기 때문에, 단사함수로 만들기 위해 정의역을 [-π/2, π/2]로 해줍니다.
다음과 같은 이유로 코사인은 공역이 [-1,1], 정의역이 [0,π]입니다. 정의역이 다른 이유는 단사함수가 되야 하기 때문입니다.
다음으로 탄젠트 또한 주기함수이기 때문에 단사함수로 만들어주기 위해, 정의역만 [-π/2, π/2]로 만들어주면 됩니다.
그래프로 나타내면 각각 다음과 같은 그래프가 나오게 됨을 알 수 있습니다. (왼쪽의 함수와 해당하는 색의 그래프로 나타냈습니다.)

수식으로는 다음과 같이 쓰고, 순서대로 아크사인, 아크코사인, 아크탄젠트라고 부릅니다.

마지막으로 다룰내용은 삼각함수의 역수로 정의된 함수를 알려드리겠습니다. 우선 그 함수들은 다음과 같이 정의됩니다.

표기는 위와 같이 하고, 순서대로 코시컨트, 시컨트, 코탄젠트라고 부릅니다.
그래프는 다음과 같이 그려집니다.

마지막으로 공식 몇 가지만 보시고 오늘 준비한 내용은 끝내도록 하겠습니다!^^




이 그림처럼 기억하시면서 위의 식들을 기억하도록 합시다. 좋은 하루 되세요!
| 질문이 있거나 틀린 부분이 있다면 언제든 댓글 달아주셔도 됩니다!! 좋아요도 눌러주시면 감사드리겠습니다 ㅎㅎ |
'미분적분학' 카테고리의 다른 글
| 극한의 엄밀한 정의-엡실론 델타 논법(쉽게 다가가보자) (0) | 2020.12.21 |
|---|---|
| 삼각함수 덧셈정리 증명 (0) | 2020.11.24 |
| 함수-함수의 결합, 역함수(+전,단사함수) (0) | 2020.11.16 |
| 함수(2) (0) | 2020.11.10 |
| 함수 (0) | 2020.11.08 |




댓글