이번 시간은 함수의 결합과 역함수에 대해서 배워보도록 하겠습니다.
목차
※ 목차를 누르면 해당 위치로 이동합니다.
함수-함수의 결합
이번 시간에는 함수를 결합하는 방법을 크게 두 가지에 대해 배우도록 하겠습니다.
'결합'이라는 단어가 어렵게 들리실 것 같긴 한데, 배우면 누구나 알고 있는 내용이고 혹시 모르는 내용이 나오더라도 쉽게 이해할 수 있으실 겁니다.
먼저 첫 번째로는 사칙연산을 통한 함수의 결합입니다.
사칙연산을 통해 함수를 결합하는 방법은 다음과 같습니다.

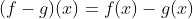
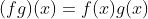

사칙연산을 통해 함수를 합칠 때는 주의할 점이 있습니다. 우선 합, 차, 곱으로 결합된 함수의 정의역은 함수 f와 g 각 함수 정의역의 공통부분이 되지만 나눗셈으로 결합된 함수는 분모가 0이 되지 않아야 하기 때문에 함수의 정의역이 g(x)가 0이 될 때는 제외되어야 한다는 것을 기억하시면 되겠습니다.
두 번째로 함수를 결합하는 방법은 합성함수로 만들어주는 법입니다. 합성함수의 표기는 다음과 같이 합니다.
\(f\circ g(x)\), \(f(g(x))\)
처음 배우신다면 어려워 보일 수도 있지만, 사실 어렵지 않은 내용입니다.
단순히 f라는 함수 안에 x대신 g라는 함수를 대입시켰다고 생각하시면 될 것 같습니다.
예시를 통해 쉽게 이해해 보도록 하겠습니다.
\(f(x)=2x\)
\(g(x)=x^2\)
이 두 개의 함수를 합성합수로 결합하면 f(g(x))는 f(x) 안에 g(x)를 대입해야 합니다. 즉, 위의 f(x)식에서 x자리에 g(x)를 넣는 것입니다.
다음 식을 보면 좀 더 이해가 쉬울 겁니다.
\(f(g(x))=2(g(x))=2(x^2)\)
역함수
함수의 결합은 여기까지 알아보도록 하고, 다음으로는 역함수에 대해서 알아보겠습니다.
우선 역함수에 대해서 알기 전에 전사함수와 단사함수에 대해서 알아야 합니다.
전사함수, 단사함수
전사함수
먼저 전사함수의 정의는 다음과 같습니다.
'함수 f : X -->Y에 대하여 Y에 속하는 모든 원소 y에 대해 f(x)=y를 만족하는 x∈X가 존재할 때 이 함수를 전사함수라 부른다.'
우선 예전에 함수에 대해 공부할 때, \(f : X \rightarrowY\)에서 Y라는 것을 공역이라 했습니다. 그리고 정의역 x에 대해 나타나는 값 f(x)의 집합을 치역이라고 했죠.
(혹시 공역과 치역의 차이가 이해가 잘 안 된다면 아래의 포스팅을 참고하시면 되겠습니다.)
함수
함수의 정의는 '어떤 집합 X에서 어떤 집합 Y로의 대응'으로 정의됩니다. 기호로는 로 정의합니다. 'X를 f의 정의역, Y를 공역이라고 부르며, f(x)를 f에 의한 x의 상이라고 부르며, 그러한 상의 집합
gonbuine.tistory.com
즉, 위에서 'Y(공역)에 속하는 모든 원소 y에 대해 (치역)f(x)=y를 만족하는 x∈X가 존재할 때'라는 말은 해석하면 공역과 치역이 일치하게 하는 정의역이 존재할 때라는 말입니다.
여기서 치역은 정의역을 f(x)에 넣었을 때 나오는 값들의 집합이므로 그냥 공역과 치역이 같은 함수를 전사함수라고 부르겠다는 얘기이죠.
예를 들어보겠습니다.
먼저 \(y=x^2\)은 전사함수일까요?
먼저 위의 포스팅에서 함수에 대해 공부하며 공역에 대해 따로 정의가 되어있지 않다면, 공역은 그냥 모든 실수로 본다고 했는데요. (평상시에는 그냥 공역에 대해 따로 정의되어 있지 않으면, 사실상 문제 풀이에 영향을 주는 경우가 거의 없기 때문에 공역=치역으로 보지만 원래는 실수 전체로 보는 것이 맞습니다.)
위의 함수의 치역은 [0~∞)입니다. 모든 치역에 대해 정의역이 모두 존재하지만 공역과 치역이 일치하지 않기 때문에 전사함수가 아니게 됩니다. 만약 전사함수가 되게 하고 싶다면, 공역을 [0,\(\infty\))으로 조절해주어야 합니다.
하지만 \(y=x\)라는 식을 보면 어떨까요?
이 함수는 공역과 치역이 일치하죠. 공역은 그냥 실수 전체라고 했을 때, 정의역도 따로 정의하지 않았기 때문에 실수 전체이고 치역 또한 실수 전체임을 알 수 있습니다. 그렇기 때문에 y=x는 전사함수입니다.
단사함수
다음으로 단사함수의 정의를 알아봅시다.
'함수 f : X -->Y에 대해 X에 속하는 서로 다른 두 원소 x,x'에 대해 f(x)≠f(x')를 만족할 때 이 함수를 단사함수라 한다.'
여기서는 어떤 함수가 임의의 x에 대응하는 y값들이 같지 않다면, 그 함수를 단사함수라고 부른다는 내용입니다. 식으로 설명하면 조금 더 와닿을 것 같습니다. 즉, 단사함수는 x≠x' --> f(x)≠f(x')인 함수입니다. 똑같은 말로 들릴 수 있을 것 같네요. 예시를 통해서 조금 더 쉽게 이해해 봅시다.
예시)

이 함수는 모든 정의역에 대해 함숫값이 다릅니다. 이런 함수를 보고 단사함수라고 부르죠.
다른 예시를 하나 들어봅시다. 다음은 어떤 함수를 그래프로 나타냈습니다.

이 함수를 보면 y=0이 되는 지점을 보면 3군데나 있는 것을 알 수 있습니다. 즉, 서로 다른 x값에 대해 같은 y값을 갖는 지점들이 있죠? 이런 함수들은 단사함수가 될 수 없는 것입니다.
전단사함수
여기까지가 전사함수와 단사함수의 설명이고 마지막으로 위에서 들었던 예시 중 y=x를 갖고 와서 잠시 다시 한번 설명하고 넘어가도록 하겠습니다.
이 함수는 어떤 함수일까요?
네, 맞습니다. 바로 제목을 보면 알 수 있듯이 이 함수는 전단사함수라고 하는데요. 이유는 모든 공역에 대해 모든 치역이 대응되고 동시에 다 다른 치역의 모든 원소가 서로 다르기 때문입니다.
이와 같이 전사이면서 단사인 함수 전단사함수를 '일대일 대응함수'라고 부릅니다.
여기까지가 전사함수와 단사함수에 대한 설명입니다. 이제는 역함수에 대해 알아보도록 하겠습니다.
역함수
우선, 역함수는 다음과 같이 정의합니다.
'함수 f : X -->Y에 대해 모든 x∈X, y∈Y에 대해 f(g(y))=y, g(f(x))=x를 만족하는 함수 g를 f의 역함수라 부른다. 이때 함수 g는 g: Y -->X를 만족한다.'
위와 같은 역함수는 다음과 같이 씁니다.

(여기서 \(f^{-1}\)은 1/f라는 의미가 아니라 f의 역함수라는 뜻입니다. 간혹 이에 대해 오해의 여지가 있을 수 있어 문제나 논문을 볼 때는 문맥에 따라 올바르게 읽는 것이 중요합니다.)
위의 정의를 이번에도 풀어서 보도록 하겠습니다.
먼저 위에서 f(g(y))=y를 볼 수 있는데요. f : X -->Y라고 했기 때문에 원래 f(x)=y임을 알 수 있습니다.
따라서 f(g(y))가 y가 나오려면 g(y)=x 라는 것을 알 수 있습니다. 또한 g(f(x))=x를 만족하게 됩니다.
그럼 f(x)=y, g(f(x))=x가 되게 하는 g는 어떤 함수일까요?
먼저 g(y)=x라는 함수를 y에 대해 정리한 함수를 y=k(x)라고 해봅시다. 그럼 우리는 f(x)=y=k(x)인 것을 알 수 있습니다.
즉, g(x)는 f(x)=y에서 x에 대해 정리한 뒤, x와 y를 바꾼 식인 것을 알 수 있습니다. 여기서 g(x)를 f(x)의 역함수라고 하고 \(f^{-1}(x)\)라고 표시하는 것이죠.
이것은 일반적으로 역함수를 만드는 방법으로 소개되는 y=f(x)에서 x와 y를 바꾸고 y에 대해 정리하는 것과 같습니다.
조금 더 설명하자면, 이 말은 \(f(x)\)와 \(f^{-1}(x)\)는 정의역과 공역이 서로 정반대인 함수라는 것입니다. 예를 들면 f(x)의 정의역이 [-\(\infty\), \(\infty\)]이고 공역이 [0,\(\infty\)]인 함수라면, g(x)의 정의역은 [0,\(\infty\)]일 때, 공역은 [-\(\infty\), \(\infty\)]으로 나타나게 되죠.
그렇다면, 전단사 함수는 왜 배웠냐고 물으신다면, 역함수로 만들기 위한 함수 f는 일대일 대응함수이어야 하기 때문이어야 합니다.
왜 그럴까 생각해 보면, 첫 번째로 전사함수여야 하는 이유는 함수의 정의는 \(X\rightarrow Y\)인데, 만약 전사함수가 아닌 경우에는 공역이 치역보다 큰 경우, \(Y\rightarrow X\)가 되었을 때, Y를 대응시킬 수 있는 X가 존재하지 않기 때문에 역함수는 함수가 될 수 없습니다.
그리고 동시에 단사함수여야 하는 이유는 함수는 하나의 x에는 하나의 y가 존재해야 하기 때문입니다. 즉, 여러 개의 x가 하나의 y에 대응되는 것은 돼도 반대는 안됩니다. 만약 x≠x' --> f(x)=f(x')라면 역함수로 바꿨을 때, f(x) \(\rightarrow\) x,x'가 되어 함수가 되지 못합니다.
그렇기 때문에 어떤 함수 f(x)를 역함수로 바꾸기 위해서는 f(x)가 전단사함수여야 하는 것입니다.
예시로 역함수를 만들어 봅시다.
\(y=x^2\)이라는 함수를 역함수로 만들어 봅시다.
이 함수는 그대로만 보면 전사함수도 단사함수도 아닙니다. 하지만 위에서 설명했듯이 우리는 정의역과 공역의 범위에 따라 전사함수나 단사함수가 될 수 있는 것을 확인할 수 있었습니다.
이를 위해, 우리도 위의 함수 자체의 역함수를 찾는다기보다는 역함수가 될 수 있는 부분만큼의 영역을 설정해 위의 함수를 역함수로 바꾸어 줄 것입니다.
그렇다면, 이 함수를 전단사 함수로 만들기 위해 정의역을 (-∞,0] 혹은 [0,∞)로 설정해 줍시다. 그리고 공역도 [0,∞)로 설정해 주도록 합시다.
그러면 전단사 함수가 되게 되죠? 그럼 그 상태에서 y와 x의 위치를 바꾸면 \(x=y^2\)이므로 \(y=\pm\sqrt{x}\)임을 알 수 있습니다.
그럼 여기서 공역과 정의역이 서로 바뀌기 때문에 역함수의 공역이 (-∞,0]인 경우에는 \(-\sqrt{x}\), [0,∞)인 경우에는 \(\sqrt{x}\)가 되는 것을 알 수 있습니다.
다시 한번 역함수 만드는 법에 대해 정리해 보도록 합시다.
- 정의역과 공역을 설정해 준다.
- x와 y의 자리를 바꾼다.
- y에 대한 함수로 다시 정리해 준다.
- 정의역과 공역에 맞추어 함수를 정리한다.
마무리로 역함수의 성질 세 가지만 배우고 마치도록 하겠습니다.



위의 세 가지 성질은 역함수에 대해 충분히 이해하셨다면, 그대로만 따라 해 보면 증명되기 때문에 증명은 하지 않도록 하겠습니다. 혹시라도 궁금하시다면, 질문해 주시면 감사하겠습니다. 언제든 답변해 드리겠습니다. ㅎㅎ
그럼 오늘은 여기서 마치도록 하겠습니다!
| 질문이 있거나 틀린 부분이 있다면 언제든 댓글 달아주셔도 됩니다!! 좋아요도 눌러주시면 감사드리겠습니다 ㅎㅎ |
'미분적분학' 카테고리의 다른 글
| 극한의 엄밀한 정의-엡실론 델타 논법(쉽게 다가가보자) (0) | 2020.12.21 |
|---|---|
| 삼각함수 덧셈정리 증명 (0) | 2020.11.24 |
| 삼각함수-(삼각함수의 성질과 역함수), 둔각삼각형 (0) | 2020.11.20 |
| 함수(2) (0) | 2020.11.10 |
| 함수 (0) | 2020.11.08 |




댓글