안녕하세요. 오늘은 이상 적분에 대해 알아보도록 하겠습니다.
먼저 이상 적분이란 우리가 정적분에서 배웠던 적분이 아닌 특이한 경우에서의 적분을 말하는데요.
이상 적분은 다음과 같이 크게 2가지의 경우로 분류합니다.
1. 함수 f가 폐구간 [a,b]에서 정의되지 않은 점을 포함하는 경우
2. 적분 구간이 유계가 아닌 경우
즉, 적분 구간이 정상적이지 않은 경우에서의 적분을 하는 것인데요.
단순히 생각했을 때는 적분이 되지 않을 것 같지만, 사실 이런 상황에서도 적분이 되는 것이 있기도 합니다.
오늘은 이런 적분들에 대해 정적분 하는 방법에 대해 배워보도록 하겠습니다.
함수 f가 폐구간 [a,b]에서 정의되지 않은 점을 포함하는 경우
먼저 1의 경우는 어떤 경우들이 있을까요?
첫 번째로 구간 내에서 정의되지 않은 점이 있는 경우, 두 번째로 점근선이 있는 경우 이렇게 나눠볼 수 있습니다.
그 중에서 우리는 두 번째인 점근선을 갖는 경우에 대해 적분을 하는 방법을 알아볼 것입니다.
말로만 설명하면, 이해가 어려울 수 있으니 그림을 보도록 하겠습니다.
이건 먼저 첫 번째 경우이고

밑에 것이 우리가 오늘 배워서 앞으로 적분을 시도할 함수들의 모형입니다.
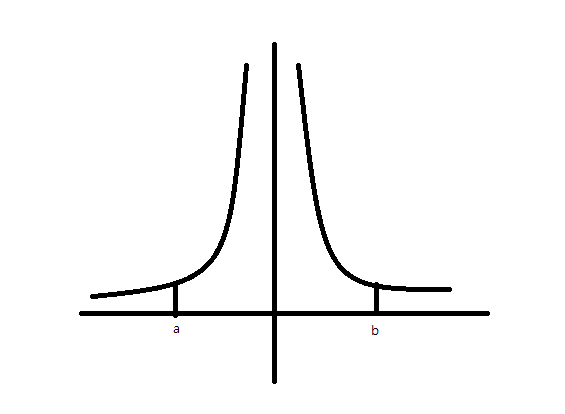
이런 식으로 x=0에 점근선이 있는 것을 볼 수 있습니다.
이런 경우에는 원래라면 [a,0]과 같은 범위로 적분을 한다면 적분값이 무한대가 나와야 할 것 같은데요.
함수에 따라서는 값이 수렴이 되어 극한값이 존재하는 경우들이 있습니다.
이러한 함수들을 적분하는 방법은 우선 간단합니다.
위의 함수를 예시로 들어보겠습니다.
만약 위의 함수를 [a,0] 구간에서 적분을 한다고 해봅시다.
그러면 \(\int^0_af(x)dx=\lim_{\epsilon \rightarrow 0^+}\int^{0-\epsilon}_af(x)dx\)과 같이 계산을 해주시면 됩니다.
좀 더 설명을 하자면, 그냥 우리가 미적분의 기본 정리에서 배운 것처럼 정적분을 해주고 위처럼 원시 함수에 엡실론을 추가한 뒤 극한값을 구해주면 됩니다.
만약 위의 그림에서 오른쪽 구간을 적분하고 싶다면, 반대로 구간을 바꾸고 다음과 같이 엡실론을 더해주면 되겠습니다.
\[\int^b_0f(x)dx=\lim_{\epsilon \rightarrow 0^+}\int^{b}_{0+\epsilon}f(x)dx\]
만약 점근선이 0이 아닌 다른 상수라면 마찬가지로 \(c\pm\epsilon\)에 대해 구해주시면 됩니다.
근데 여기서 주의하셔야 할 것이 있습니다.
바로 점근선이 구간 끝이 아닌 구간 사이에 있는 경우입니다.
이러한 경우에는 점근선을 기준으로 양 옆 구간을 더하는 방식을 이용해 이상 적분을 구하게 되는데요.
원래는 다음과 같은 식을 사용해서 이상 적분을 구해야 합니다.
\[\int^b_af(x)dx=\lim_{\epsilon \rightarrow 0^+}\int^{b}_{0+\epsilon}f(x)dx +\lim_{\epsilon' \rightarrow 0^+}\int^{0-\epsilon'}_af(x)dx\]
근데 여기서 어떤 분은 아래의 식을 보고 '이런 식으로 구해도 되지 않나?' 싶을 수도 있습니다.
하지만 이 방식은 틀린 방법입니다.
\[\int^b_af(x)dx=\lim_{\epsilon \rightarrow 0^+}\left\{\int^b_{0+\epsilon}f(x)dx+\int^{0-\epsilon}_af(x)dx\right\}\]
그 이유는 이런 경우에는 점근선을 기준으로 끊어서 양 옆 구간에 대해 따로 계산을 해야 하기 때문입니다.
만약 이렇게 계산을 하면 언제나 양 구간에 대해 각각 따로 구한 뒤 더한 값이 나와야 할텐데요.
하지만 아래의 식으로 계산을 하면 다른 값이 나오는 경우가 있습니다.
예를 들어보도록 하겠습니다.
\(f(x)=\frac{1}{x}\)라는 함수를 폐구간 [-1,1]에서 적분해보도록 합시다.
그러면 한 번 해보면 알텐데요. 원래 방식은 \(-\infty+\infty\)가 나오는데 반해, 아래 방식을 이용하면 0이 나오는 것을 알 수 있습니다.
각각 더했을 때, 발산인 것과 달리 아래 방식을 쓰면 수렴하는 결과가 나올수도 있는 것이죠.
만약 왜 0이 되면 안되는지 궁금하신 분들은 \(\lim_{x \rightarrow \infty}x+\lim_{x \rightarrow \infty}-x\)에 대해 계산해보시면 좋을 것 같습니다.
이것은 0처럼 보일 수도 있지만 사실 둘 다 극한값이 없기 때문에 우리가 앞서 배운 극한의 분배 법칙을 사용할 수 없는데요.
그렇기 때문에 그냥 무한과 무한끼리의 계산이고 서로 계산할수가 없게 됩니다.
궁금하다면 이에 대해 따로 정리하도록 하겠습니다.
적분 구간이 유계가 아닌 경우
이건 쉽게 말해 적분 구간이 \(\infty\)나 \(-\infty\)를 포함하는 경우를 말합니다.

막상 봤을 때는 어떻게 하는거지 하실 수도 있지만 이것도 방식은 위와 같이 너무 간단합니다.
이것도 마찬가지로 미적분의 기본 정리를 이용해 단순히 원시함수에 대체값을 넣고 극한을 계산하는 것이죠.
다음과 같이 계산을 하면 됩니다.
구간이 양의 방향으로 무한인 경우
\[\int_{a}^{\infty}f(x)dx=\lim_{c \rightarrow \infty}\int^c_af(x)dx\]
구간이 음의 방향으로 무한인 경우
\[\int_{-\infty}^{b}f(x)dx=\lim_{c \rightarrow -\infty}\int^b_cf(x)dx \]
그런데 이것도 주의할 점이 있습니다.
바로 적분구간이 양 방향으로 무한인 경우인데요.
이런 이상 적분의 경우에는 아래 방법을 이용해 이상 적분을 해야합니다.
\(\int_{-\infty}^{\infty}f(x)dx=\lim_{b \rightarrow -\infty}\int^a_bf(x)dx+ \lim_{c \rightarrow \infty}\int^c_af(x)dx\)
이렇게 두 영역으로 나눠주는 이유는 어떤 점을 기준으로 양 쪽 구간을 더한 값과 적분값이 같아야 하기 때문입니다.
만약 다음과 같이 적분을 한다면 잘못된 값이 나올 수 있게 됩니다.
\(\int_{-\infty}^{\infty}f(x)dx=\lim_{b \rightarrow \infty}\int^b_{-b}f(x)dx\)
예를 들어 \(f(x)=x^3\)인 경우에 대해 계산을 해보도록 하겠습니다.
먼저 아래 방법으로 계산해보겠습니다.
\[\lim_{b \rightarrow \infty}\int^b_{-b}x^3dx=\lim_{b \rightarrow \infty}\left[\frac{1}{4}x^4\right]^b_{-b}=\lim_{b \rightarrow \infty}0=0\]
하지만 어떤 점을 기준으로 양 쪽의 적분값을 더해주면 값이 변하게 됩니다.
\[\lim_{b \rightarrow \infty}\int^0_{-b}x^3dx+\lim_{b \rightarrow \infty}\int^b_0x^3dx=-\infty+\infty\]
즉, 수렴이 되면 안되는 함수가 수렴이 되기 때문에 아래의 방식을 이용하면 안됩니다.
이상 적분 수렴, 발산 판별
간혹 이상 적분이 적분 가능한지 알아보아야 하는 경우들이 있습니다.
하지만 이때 부정적분 자체가 어려운 함수들은 직접 계산하는 방법으로는 구하기가 어려운데요.
이 때 이상 적분의 수렴, 발산을 판정하기 위해 사용하는 방법이 있습니다.
바로 비교 판정법이라는 것인데요.
이건 샌드위치 정리와 원리가 같습니다.
원리는 다음과 같습니다.
| 이상 적분 비교판정법 연속 함수 f,g가 있을 때, a\(\leq\)x인 구간에서 0\(\leq\)g(x)\(\leq\)f(x)라면 다음을 만족한다. 1) \(\int^{\infty}_af(x)dx\)가 수렴하면 \(\int^{\infty}_ag(x)dx\)도 수렴한다. 2) \(\int^{\infty}_ag(x)dx\)가 발산하면 \(\int^{\infty}_af(x)dx\)도 발산한다. |
즉, 쉽게 설명하면 f가 g보다 크다면 f가 수렴하면 g도 수렴하고 g가 발산한다면 f도 발산한다는 것입니다.
왜 그럴까요. 이유는 간단합니다. 말 그대로 f가 g보다 큰데 f는 어떤 수를 향해 수렴하는데 g가 더 커지거나 진동하면 f보다 작을 수 없고 반대로는 더 작은 g가 발산하고 f가 수렴할 수 없기 때문입니다.
원리는 이렇고 실제로 한번 적용해보도록 해봅시다.
\[\int^{\infty}_2e^{-x^2}\]
만약 위와 같은 함수가 있다고 해봅시다.
이 함수는 수렴할까요? 발산할까요?
먼저 적분을 해보도록 합시다. 근데 생각보다 부정적분 자체가 쉽지 않습니다.
이 때 다른 함수와 비교를 해볼 수 있습니다.
저는 왠지 \(e^{-x}\)와 비교해보고 싶네요.
그럼 x가 2보다 큰 구간 내에서는 \(0\leq e^{-x^2}\leq e^{-x}\)이기 때문에 계산해보면 같은 구간에서 \(e^{-x}\)는 수렴하는 것을 알 수 있고 따라서 \(e^{-x^2}\)도 수렴하는 것을 알 수 있습니다.
이렇게 이상 적분에 대한 기본적인 개념에 대해 같이 알아볼 수 있었는데요.
개념적인 부분에서 궁금한게 있었던 분이라면 오늘 포스팅을 통해 해결되었으면 좋겠습니다.
만약 이해가 가지 않는 부분이 있다면 댓글 남겨주시면 최대한 답변드리도록 하겠습니다.
다음 시간에 봐요~
'미분적분학' 카테고리의 다른 글
| 기타 적분법(삼각함수, 무리함수) (0) | 2023.01.24 |
|---|---|
| 부분분수 만드는 법 (0) | 2023.01.19 |
| 삼각치환법 개념 (0) | 2023.01.18 |
| 치환적분, 부분적분 개념 및 요약 (2) | 2023.01.18 |
| 쌍곡선 함수와 역쌍곡선 함수 (0) | 2023.01.16 |




댓글