목차
※ 목차를 누르면 해당 위치로 이동합니다.
자연상수 e와 용도
안녕하세요. 오늘은 지수함수와 로그함수의 도함수에 대해 배워보도록 하겠습니다.
하지만 이에 대해 배우기 전에 알아야 하는 게 있는데요. 바로 자연상수 e입니다.
이 자연상수는 오일러가 발견한 것으로 알려진 상수로 자연의 현상들을 수식으로 나타내거나 다양한 수식들을 증명하는데 중요한 역할을 하고 있습니다.
자연상수의 정의는 다음과 같습니다.
| 자연상수 e \[e=\lim_{x \rightarrow \infty}\left(1+\frac{1}{x}\right)^x\] |
자연상수의 대표적인 예로는 이자에 대한 이야기를 들 수 있습니다.
경제를 조금이라도 알고 계신다면 다들 한 번쯤은 복리에 대해 배워보신 적 있을 겁니다.
예를 들어 500원을 은행에 맡겼다고 해봅시다. 만약 이때 은행이자가 연 5%라고 한다면, 우리가 총 받을 수 있는 돈은 다음과 같이 수식으로 쓸 수 있습니다.
\((500\cdot\frac{105}{100})\frac{105}{100}\cdot\frac{105}{100}...\)
\(=500\cdot (1+\frac{5}{100})^{year}\)
근데 만약 은행이자를 연 5%가 아니라 매일 5%를 준다고 하면 여러분들은 1년만 있어도 2백억 가량의 돈을 모을 수 있게 됩니다.
근데 이런 일은 말도 안 되죠. 그렇기 때문에 만약 여러분들에게 은행이자를 매일 주게 된다면, 간단히 생각하면 은행에서는 연 이자의 매일 1/365만큼의 이자를 받게끔 줄 것입니다.
즉, 1년에 받는 수익은 다음 수식과 같을 텐데요.
\(500\cdot(1+\frac{0.05}{365})^{365(일)}\)
이것은 약 525.6원의 돈과 같습니다. 근데 잠시 이 식을 보면 어떤 식과 비슷해 보이지 않나요?
네, 이 식은 위에서 말한 자연상수 e와 유사한 식인데요.
자연 상수 e의 정의를 보면 분모의 수와 지수가 계속해서 커지는데요. 즉, 하나만 커지는 게 아니라 둘 다 같이 무한대로 가면 자연 상수 e로 수렴을 한다는 것입니다.
이와 마찬가지로 위의 525.6원도 보면 원래 연 5%의 이자인 이자와 (좀 계산해 보면) 0.1% 이자 차이밖에 안 나게 되는 것을 알 수 있습니다.
그리고 수를 더 늘려서 같은 논리로 하루에 세 번씩 이자를 준다고 하면 계산기를 이용해 계산하면 똑같이 거의 0.002%의 차이밖에 안나는 것을 알 수 있는데, 이처럼 은행이나 다양한 곳에서 자연상수 e의 원리를 이용해 무언가를 계산하기도 합니다.
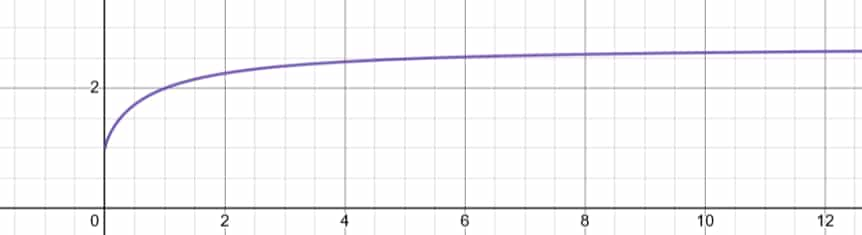
또 다른 예를 들면, 어떤 식물의 성장 가능 최대치와 같이 처음에는 급격하게 늘어나지만 한계가 정해진 것들을 구할 때 자연 상수를 이용해 구하기도 합니다.
자연로그, 상용로그
이와 관련해 로그의 밑에 따라 불리는 이름이 정해진 특별한 로그들이 있습니다.
그중 밑이 자연 상수 e인 로그를 자연로그, 밑이 10인 로그를 상용로그라고 부르고 기호는 각각 ln, log(밑 생략)와 같이 적습니다.
\[log_e=ln, log_{10}=log\]
그런데 우리나라에서는 이렇게 표기하지만 몇몇 나라에서는 이를 반대로 표기하는 나라들도 있는데요. 그렇기 때문에 외국 논문이나 책을 볼 때는 밑이 e인지 10인 로그를 말하는지 앞뒤 수식에 따라 잘 파악하는 것이 좋습니다.
로그함수의 도함수
먼저 로그함수의 도함수는 다음과 같습니다.
| 로그함수의 도함수 1) \((ln\mid x\mid)'=\frac{1}{x}\) 2) \((ln\mid f(x)\mid)'=\frac{f'(x)}{f(x)}\) 3) \((log_a\mid x\mid)'=\frac{1}{xlna}\) 4) \((log_a\mid f(x)\mid)'=\frac{f'(x)}{f(x)lna}\) |
잠시 증명을 하기 전에 한 가지 알아야 할 것이 있습니다. 위에서 보면 각각 절댓값이 씌워져 있는 것을 볼 수 있는데요.
물론 보통 로그함수의 경우에는 x가 0보다 커야 하지만, 허수를 포함하는 경우에는 x가 0보다 크지 않은 경우들도 있기 때문에 위의 증명들은 모두 실수에 한해서 증명하기 위해 절댓값을 포함한 것이라고 아시면 될 것 같습니다.
증명은 다음과 같습니다.
1)
x>0인 경우,
\(\frac{\triangle y}{\triangle x}=\frac{1}{\triangle x}[ln(x+\triangle x)-lnx]\)
=\(\frac{1}{\triangle x}ln\frac{x+\triangle x}{x}=\frac{1}{x}\frac{x}{\triangle x}ln\left(1+\frac{\triangle x}{x}\right)\)
=\(\frac{1}{x}ln\left(1+\frac{\triangle x}{x}\right)^{x/\triangle x}\)
\(\lim_{\triangle x \rightarrow 0}\frac{\triangle y}{\triangle x}=\lim_{\triangle x \rightarrow 0}\frac{1}{x}ln\left(1+\frac{\triangle x}{x}\right)^{x/\triangle x}\)
여기서 이 식은 다음과 같이 바꿀 수 있으므로 아래와 같이 자연상수 e가 되게 됩니다. (수식이 다름에도 자연상수가 되는 이유는 자연상수 용도에서 다룬 것처럼 분모가 커짐에 따라 지수가 똑같은 값으로 커지기 때문입니다.)
\(\lim_{\triangle x \rightarrow 0}\left(1+\frac{\triangle x}{x}\right)^{x/\triangle x}=\lim_{x/\triangle x \rightarrow \infty}\left(1+\frac{\triangle x}{x}\right)^{x/\triangle x}=e\)
\[\therefore y'=\lim_{\triangle x \rightarrow 0}\frac{\triangle y}{\triangle x}=\frac{1}{x}lne=\frac{1}{x}\]
x<0인 경우
f(x)=-x라고 하면
\(y'=\frac{1}{-x}\cdot (-x)'=\frac{1}{x}\)
2) x<0인 경우에서 설명한 것처럼 합성함수 미분법을 이용하면 증명할 수 있습니다.
3) \((log_a\mid x\mid)'=\left(\frac{ln\mid x\mid}{lna}\right)'=\frac{1}{xlna}\)
4) 또한 합성함수 미분법을 이용하면 쉽게 증명할 수 있습니다.
2,4를 굳이 쓴 이유는 문제를 풀다 보면 f(x)를 로그에 대입해서 풀어야 하는 경우들이 있을 텐데, 이때 별생각 없이 풀다 보면 절댓값을 취하지 않는 경우들도 있습니다.
정의역은 보통 문제에서 당연히 x>0인 경우에 대해 푸는 경우가 많지만 f(x)는 대입하다 보면 음수에 대해서도 대입을 하는 경우가 많기 때문에 될 수 있으면 f(x)를 대입할 때 절댓값을 떠올렸으면 좋겠어서 강조 차원으로 같이 넣어봤습니다.
그럼 지수함수로 넘어가 보겠습니다.
지수함수의 도함수
지수함수의 도함수는 다음과 같습니다.
| 지수함수의 도함수 1) \((a^x)'=a^xlna\) 2) \((e^x)'=e^x\) |
1) \(y=a^x\)에서 양변에 자연로그를 넣으면 \(lny=xlna\)이고, 이것을 x에 대해 미분하면 \(\frac{y'}{y}=lna\)이기 때문에 y를 오른쪽으로 넘기면 \(y'=a^xlna\)가 되게 됩니다.
2) 마찬가지로 a에 e를 넣으면 증명이 됩니다.
오늘은 로그함수의 도함수와 지수함수의 도함수에 대해 알아보았는데요. 도움이 되셨나요? 혹시라도 이해가 안 되거나 어려운 부분이 있다면 댓글 남겨주시면 빠르게 답변해 드리도록 하겠습니다.
그럼 오늘 포스팅은 여기까지 하도록 하고 다음 포스팅에서 다시 뵙겠습니다.
열공하세요~
'미분적분학' 카테고리의 다른 글
| 치환적분, 부분적분 개념 및 요약 (2) | 2023.01.18 |
|---|---|
| 쌍곡선 함수와 역쌍곡선 함수 (0) | 2023.01.16 |
| 지수함수와 로그함수(+로그함수의 다양한 성질) (0) | 2023.01.11 |
| 무게 중심(질량 중심)과 모멘트 (2) | 2023.01.08 |
| 회전체의 겉넓이 구하기 (0) | 2023.01.05 |




댓글