이번 시간에는 테일러급수라는 것에 대해 알아보도록 하겠습니다.
테일러급수의 이해
먼저 테일러급수란 어떤 함수이든지 다항함수 꼴로 만들기 위해 사용되는 수학적 도구입니다.
이렇게 하는 이유는 계산을 하는 많은 경우에 다항함수가 편리하기 때문입니다.
예를 들어 아래와 같은 함수가 있다고 가정합시다.
\(f(x)=sinx+e^x+lnx\)
\(f(x)=x^2+3x+5\)
자 어떤가요? 물론 어떤 계산을 할지에 따라 다르겠지만, 아래 함수가 더 간단해 보이지 않나요?
실제로 단순히 미적분만 하더라도 다항함수를 이용하는 게 대부분 계산이 쉽습니다.
테일러급수는 이런 편리함 때문에 실제로 물리학, 컴퓨터 공학 등 다양한 곳에 자주 사용되기도 합니다.
어찌 됐든 테일러급수에 대해 알아보도록 하겠습니다. 테일러급수란 무엇일까요?
테일러급수의 정의는 다음과 같습니다.
| 테일러 급수 열린 구간 (a,b)에서 f(x)가 무한히 미분 가능하면, 함수 f(x)는 다음과 같이 표현 가능하다. \[f(x)=\sum_{n=0}^\infty \frac{f^{(n)}(a)}{n!}(x-a)^n\] |
증명을 하기 전에 위에서 \(f^{(n)}(a)\)라는 표현이 이해가 잘 가지 않았을 수도 있는데요. 이것은 함수 f를 a라는 점에서 n번 미분했다는 소리입니다.
그러면 돌아와서 바로 증명을 해보도록 하겠습니다.
먼저 위에서 테일러급수는 어떤 함수를 다항함수 꼴로 나타내기 위해 사용되는 수학적 도구라고 했었는데요. 먼저 어떤 함수를 다항함수로 나타낼 수 있다면 다음과 같이 적을 수 있을 겁니다.
\(f(x)=c_0+c_1(x-a)+c_2(x-a)^2+c_3(x-a)^3+...+c_n(x-a)^n\)
여기서 우리가 구해야 하는 것은 앞에 붙은 \(c_n\)입니다. 먼저 함수 f를 미분해보도록 합시다.
\(f'(x)=c_1+2c_2(x-a)+3c_3(x-a)^3+...+nc_n(x-a)^n\)
그럼 여기서 x에 a를 넣으면 어떻게 될까요. \(c_1\)=\(f'(x)\)가 나오겠죠? 그럼 다시 한번 미분해보도록 합시다.
\(f''(x)=2c_2+3c_3(x-a)^3+...+nc_n(x-a)^n\)
여기서도 x에 a를 넣는다면 이번엔 약간의 계산을 통해 \(c_2\)=\(\frac{f"(a)}{2}\)를 얻어낼 수 있습니다.
이와 같은 방식으로 계속해서 \(c_n\)의 값을 구한다면, \(c_n\)은 \(\frac{f^{(n)}(a)}{n!}\)이 나오게 됩니다.
참고로 여기서 n!이라는 기호를 모르는 분들을 위해 잠시 설명을 하자면, !은 팩토리얼이라고 읽고 \(n(n-1)(n-2)...\times 2 \times 1\)을 n!과 같이 간단하게 표현할 수 있습니다.
돌아와서 위에서 구한 \(c_n\)을 다항식에 집어넣게 되면, 테일러급수의 형태와 같은 식을 보게 됩니다.
\[f(x)=\sum_{n=0}^\infty \frac{f^{(n)}(a)}{n!}(x-a)^n\]
이로 인해 우리는 함수 f가 무한히 미분 가능하다면, 테일러급수와 같은 다항함수 꼴로 만들어 낼 수 있음을 알게 됩니다.
참고로 여기서 a=0인 경우를 맥클로린 급수라고 부르는데, 이렇게 나타내면 식이 조금 더 간편해지게 됩니다.
| 맥클로린 급수 \[f(x)=\sum_{n=0}^\infty \frac{f^{(n)}(0)}{n!}x^n\] |
테일러급수의 응용
그렇다면 테일러급수는 어떤 때에 사용이 가능한 것일까요?
(1) 테일러급수의 기본적인 활용
테일러급수는 당연히 무한히 미분 가능한 함수일 때 사용 가능합니다. 그런데 테일러급수는 아무래도 급수로 표현되기 때문에 도함수가 미분이 될 때마다 규칙성을 갖는 함수일 때 사용하기 좋은데요.
예를 들면 sinx와 같은 함수의 경우 \(f^{(n)}(0)=1(4n+1),0(2n),-1(4n-1)\)와 같은 규칙성을 가지기 때문에 테일러급수에서 x가 0인 함수로 나타내면 다음과 같이 나타낼 수 있습니다.
\[sinx=\sum_{n=0}^\infty \frac{(-1)^n}{(2n-1)!}x^{(2n-1)}\]
(2) 무한히 미분 가능하지 않은 함수의 테일러급수 사용 방법
한편, 테일러급수는 경우에 따라 무한히 미분 가능하지 않아도 함수를 다항함수 꼴로 나타낼 수 있습니다.
바로 함수의 범위에 따라 이 경우가 달라지는데요.
아래 사진들에서 다항함수의 항이 많아질수록 원함수와 그래프에서 일치하는 부분이 많아지는 것이 보이는데요.
즉, 항이 무한에 가까워질수록 원함수와 가까워지고 어느 정도 범위 내에서는 같은 값을 가지므로 같은 함수로 봐도 무방하게 됩니다.


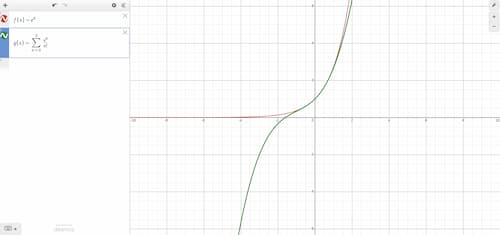

이렇게 구한 근삿값으로 일정 구역 내에서는 꼭 무한히 미분 가능하지 않더라도 테일러급수를 사용해 계산하기도 합니다.
한편, 위의 함수는 \(e^x\)의 맥클로린 급수이기 때문에 x=0에 가까운 범위부터 점점 함숫값이 비슷해지는 것을 알 수 있습니다.
'테일러급수를 사용할 때 \(f^{(n)(x)}\)에서 x에 어떤 값을 넣어도 같은 함수가 나올까?'라는 의문을 한 번쯤 가져본 적 있으실 텐데요.
이와 같이 만약 x=a라면 다항함수의 항이 늘어날수록 x=a인 점 근처부터 비슷한 함수가 나오게 됩니다.
또한 당연하게 함수가 무한히 미분 가능할 때는 x에 어떤 값을 넣더라도 같은 다항함수가 나오게 됩니다.
오늘 알아볼 내용은 여기까지 인데요. 사실 테일러급수는 미적분학의 꽃이라고 불릴 정도로 자주 사용되는 급수이기 때문에 대학교에서 이과 쪽으로 가실 분들이라면 꼭 알아두어야 할 급수 중 하나입니다. 잘 익혀두셔서 나중에 잘 사용하시기 바라겠습니다.
그럼 오늘 포스팅은 여기서 마무리하고 다음 포스팅에서 뵙도록 하겠습니다~
'미분적분학' 카테고리의 다른 글
| 곡선 사이 영역의 넓이 구하기 (1) | 2022.12.19 |
|---|---|
| 로피탈 정리의 간결한 이해와 주의점 (0) | 2022.12.12 |
| 미분이란?(미분계수, 미분의 응용) (0) | 2022.12.03 |
| 부정적분과 정적분(고등과정부터 대학과정까지 알아보자)-3 (2) | 2022.11.30 |
| 부정적분과 정적분(고등과정부터 대학과정까지 알아보자)-2 (2) | 2022.11.27 |




댓글