안녕하세요. 오늘은 삼각함수 덧셈정리에 대해 증명을 해드리려고 합니다. 개인적으로는 한 번쯤은 이 부분에 대해서 찾아보거나 하는 걸 추천드리긴 하지만, 이 부분은 증명하는법을 계속해서 외우는 것보다는 공식자체를 반복적으로 외워버리는 것을 더 추천드리네요. ㅋㅋ 제 의견일 뿐이고, 옳다고 생각하시는대로 하시면, 될 것 같습니다.
우선 덧셈정리를 증명하는 방법은 다양하게 있지만, 저는 코사인 덧셈정리를 통해 나머지 공식들을 유도해내는 식으로 증명하는 방법을 사용하도록 하겠습니다.

우선 이 글에서는 선분 AB는 그냥 AB로 표현하도록 하겠습니다. 그럼 설명을 이어가보도록 하면, 위의 그림에서 원은 단위원이라고 하고, A,B의 좌표는 각각 (cosa, sina), (cosb, sinb)라고 합시다. 그러면, AB는 좌표계에서 피타고라스 정리를 이용해 다음과 같이 쓸 수 있습니다.

2020/11/20 - [미분적분학] - 삼각함수-(삼각함수의 성질과 역함수), 둔각삼각형
위의 링크를 통해 마지막 부분을 통해 왜 사인, 코사인 제곱들이 2로 변화했는지 알 수 있습니다.
다음으로 삼각형을 -b만큼 회전시키도록 해봅시다.

여기서 원은 그대로 단위원이기 때문에, A', B' 각각의 좌표는 (cos(a-b),sin(a-b)), (1,0)으로 나타납니다.

(AB)^2=(A'B')^2을 정리하면 다음과 같습니다.

이제 여기서부터 하나씩 간단한 대입들을 통해 식들을 정리해가보도록 합시다.
먼저, b대신 -b를 대입해 코사인에서의 a+b에 대해 정리해볼까요?

코사인은 우함수이고, 사인은 기함수이기 때문에 위와 같이 변형되었습니다.
그렇다면, 이번에는 sin에 대해서 정리해보도록 해봅시다. 우선 여기서는 sinθ=cos(π/2-θ)를 이용해 보도록 합시다.
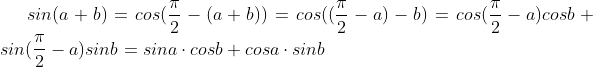
위와 같이 정리된 식에 다시 한 번 b대신 -b를 대입하게 되면,

이렇게 코사인과 사인에서의 덧셈정리를 증명할 수 있었습니다.
다음 탄젠트는 사인 함수와 코사인 함수의 덧셈정리를 이용하면, 또한 쉽게 구할 수 있습니다.

cosa*cosb(≠0)로 분자, 분모 모두 나눠주게 되면, 다음과 같은 식이 나오게 됩니다.

또한 여기서 b에 -b를 대입하게 되면, 탄젠트는 기함수이기 때문에 다음과 같은 식이 나오게 됩니다.

이렇게 삼각함수의 덧셈정리에 대해서 모두 증명해봤습니다.
사실 정리할까 고민했던 내용이었지만, 한 번 다뤄봤습니다. 정보도 다양하고, 보통은 덧셈정리는 그냥 공식만 외워서 쓰는게 보통이니깐요. 그래도 혹시라도 궁금하신 분들이 계셨다면, 도움이 됐길 바라겠습니다.
오늘 준비한 내용은 여기까지입니다. 다들 즐공하세요.^^
'미분적분학' 카테고리의 다른 글
| 부정적분과 정적분(고등과정부터 대학과정까지 알아보자.)-1 (0) | 2022.06.19 |
|---|---|
| 극한의 엄밀한 정의-엡실론 델타 논법(쉽게 다가가보자) (0) | 2020.12.21 |
| 삼각함수-(삼각함수의 성질과 역함수), 둔각삼각형 (0) | 2020.11.20 |
| 함수-함수의 결합, 역함수(+전,단사함수) (0) | 2020.11.16 |
| 함수(2) (0) | 2020.11.10 |




댓글