안녕하세요. 저번 시간에는 고등학교에서 배우는 정적분에 대해 같이 알아보았습니다. 오늘은 대학과정에서 다루는 정적분에 대해 이야기해보도록 하겠습니다.
부정적분과 정적분(고등과정부터 대학과정까지 알아보자.)-1
오늘은 적분에 대해 알아보는 시간을 가지려고 합니다. 먼저는 기본적으로 부정적분에 대해 설명하며, 정적분이란 무엇인지, 정적분을 통해 미분과 적분의 관계에 대해 배워보도록 하겠습니다.
gonbuine.tistory.com
오늘 배울 내용은 저번 포스팅 마지막 부분에서 얘기한 것처럼 정적분을 좀 더 엄밀하게 정의하는 방법에 관한 내용을 다뤄볼텐데요. 이 부분은 리만 적분에 관한 내용으로 한 번쯤 이름은 들어보셨을 수도 있는 내용입니다. 개념 자체는 막 어렵지는 않은 내용이기 때문에 끝까지 읽으시면 용어에 대해서도 자세하게 설명해놨으니 잘 이해하실 수 있을 겁니다.
리만 적분
먼저 리만 적분의 정의는 다음과 같습니다.
| 리만적분의 정의 함수 f가 폐구간 [a,b]에서 정의된 유계인 함수라고 하고 [a,b]의 임의의 분할 \(P:a=x_{0}<x_{1}<...<x_{n}=b\)에 대해 ∣P∣를 분할 크기의 최댓값으로 정의하자. 만약 임의의 분할 각 구간에서 임의의 점 \(x_i^*\)를 택하더라도 \[\lim_{\mid P\mid \rightarrow 0}\sum_{i=1}^nf(x_i^*)(x_{i}-x_{i-1})\] 이 L로 수렴한다면 f는 [a,b]에서 적분가능이라고 말하고 \[\int_{a}^{b} f(x)dx\] 로 표기한다. |
여기서 나오는 내용 중 분할이라는 내용이 생소하실 수도 있을 것 같은데요. 밑에서도 배우겠지만 분할이란 일정 범위를 여러 개로 쪼개는 것을 말합니다. 쪼개는 방법은 여러 방법이 있겠지만 우리는 그 범위에 점을 찍는 것으로 구역을 나눠주는 방법을 이용합니다. 그 점의 집합을 우리는 분할 P로 표현을 합니다.
그리고 여기서는 분할 P의 크기를 ∣P∣로 표기하고 임의의 분할 중 가장 크기가 큰 값으로 정의하는 것인데요.
여기서 임의의 점 \(x_i^*\)를 택하더라도 위의 극한값이 L로 수렴해야 함수가 적분 가능이라고 하는 말을 해석하면 임의의 분할에 대해 ∣P∣가 0으로 향할 때 밑에서 배울 상합과 하합이 같은 값으로 수렴한다는 소리입니다. 이것을 간결하게 표현하면 아래와 같이 표현할 수 있습니다.
| [a,b]에서 유계(상,하한이 있는)인 함수 f가 다음 조건을 만족하면 f는 [a,b]에서 리만적분 가능하다. \((\forall\epsilon>0)\), \(U(f,P)-L(f,P)<\epsilon\) (\(\forall\epsilon>0\)을 해석하면 임의의 양수인 ϵ에 대하여라는 의미) |
사실 분할에 대해 처음 들어보신다면 이 말들이 무슨 말인지 이해가 잘 안 가실 겁니다. 위의 설명들을 이해하기 위해서는 먼저 다음 내용들을 이해할 필요가 있습니다.
분할

분할은 위에서 말한 것처럼 일정 범위를 여러 개로 쪼개 주는 것을 말하는데요. 오늘 배울 분할의 방법은 일정 범위에 점을 찍어 구역을 나누는 방법을 이용합니다. 예를 들면 위의 그림처럼 임의의 위치에 점을 찍어줄 수 있는데요. 이러한 점들을 모아 집합 P로 만들고 다음과 같이 표현합니다.
\((P:a=x_{0}<x_{1}<...<x_{n}=b)\),\((P=x_{1}, x_{2},...,x_{n-1})\)
유계, 상한, 하한
먼저 우리는 앞으로 배울 내용들을 위해 몇 가지 표기법을 이해할 필요가 있습니다. 그중 먼저 유계, 상한, 하한에 대해서 알아볼 텐데요.
개념은 아주 간단합니다. 유계란 어떤 한계가 존재하는 것을 의미하고 상한은 그런 한계가 위로 존재하고 하한은 아래로 존재하는 것을 의미합니다. 예를 들어 만약 0≤f(x)≤1라고 가정하면, f(x)는 유계인 함수이고 1을 상한으로 가지고 0을 하한으로 가진 함수라고 합니다.
이러한 함수의 상한과 하한은 다음과 같이 표기합니다.
상한 \(sup\) \(f\)
하한 \(inf\) \(f\)
상합과 하합
다음으로 상합과 하합에 대해 알아볼 필요가 있습니다. 먼저 분할로 구간을 나누었다면 각 구간마다 구간에 해당하는 함수의 최대, 최솟값이 있을 텐데요.('만약 없다면?'이라는 생각이 든다면 완비성 공리라는 것에 대해 알아보시는 것을 추천드립니다.) 여기서 왼쪽 그림처럼 함수의 최댓값(\(M_{i}\))에 해당하는 사각형끼리 더한 것을 상합, 오른쪽처럼 함수의 최솟값(\(m_{i}\))에 해당하는 사각형끼리 더한 것을 하합이라고 합니다.


또한 이것을 기호로 다음과 같이 표기합니다.
상합(Upper sum) \[U(f,P)=\sum_{i=1}^nM_{i}(x_{i}-x_{i-1})\]
하합(Lower sum) \[L(f,P)=\sum_{i=1}^nm_{i}(x_{i}-x_{i-1})\]
그리고 상합 중에서 하한인 것을 상적분이라고 부르고 하합 중에서 상한인 것을 하적분이라고 부릅니다. 표기는 다음과 같습니다.
\[U(f)=inf\left\{U(f,P),P\in [a,b]\right\}\]
\[L(f)=sup\left\{L(f,P),P\in [a,b]\right\}\]
그리고 만약 U(f)=L(f)라면 f는 리만적분이 가능하다고 합니다.
여기까지 왔으면 위에서 말한 것을 다시 한번 생각해보도록 합시다.
| 리만적분의 정의 함수 f가 폐구간 [a,b]에서 정의된 유계인 함수라고 하고 [a,b]의 임의의 분할 \(P:a=x_{0}<x_{1}<...<x_{n}=b\)에 대해 ∣P∣를 분할 크기의 최댓값으로 정의하자. 만약 임의의 분할 각 구간에서 임의의 점 \(x_i^*\)를 택하더라도 \[\lim_{\mid P\mid \rightarrow 0}\sum_{i=1}^nf(x_i^*)(x_{i}-x_{i-1})\] 이 L로 수렴한다면 f는 [a,b]에서 적분가능이라고 말하고 \[\int_{a}^{b} f(x)dx\] 로 표기한다. |
위에서 우리는 분할에 대해 배웠으니 좀 더 이해가 편하실 것이라 생각합니다.
"만약 임의의 분할 각 구간에서 임의의 점 \(x_i^*\)를 택하더라도"
이 말은 무엇일까요. 먼저 상합은 하합보다 크거나 같습니다. 즉, 분할에서 가장 큰 상합과 가장 작은 하합이 특정 값을 향해 수렴한다면 적분 가능인 것입니다. 그럼 '상합보다 작고 하합보다 큰 것들은 어떻게 하냐?'라고 한다면 이것들은 샌드위치 정리에 의해 모두 같은 값을 향해 수렴한다고 얘기할 수 있습니다.
이것을 간단히 표현한 것이 다음과 같습니다.
| [a,b]에서 유계(상,하한이 있는)인 함수 f가 다음 조건을 만족하면 f는 [a,b]에서 리만적분 가능하다. \((\forall\epsilon>0)\), \(U(f,P)-L(f,P)<\epsilon\) (\(\forall\epsilon>0\)을 해석하면 임의의 양수인 ϵ에 대하여라는 의미) |
즉, 모든 양수 엡실론보다 상합과 하합의 차이가 작기 위해서는 0이 나와야 한다는 것입니다. 즉, \(U(f,P)=L(f,P)\)인 경우에 리만 적분이 가능하다는 것입니다. 이게 리만적분의 개념이고 전부입니다.
근데 위에서 읽다 보면 '상합은 하합보다 크거나 같다.'라는 말에서 막연하게 '정말 그럴까?'와 같은 궁금증이 생기실 수도 있습니다. 이 부분을 간단하게 증명해보도록 하겠습니다.
먼저 저 질문에 대해 답하기 위해서는 세분이라는 것을 알아야 합니다.
세분이란 어떤 분할을 보다 잘게 쪼개는 것을 말합니다. 예시를 들어보면 (P=a, x1, b)라는 분할이 있다고 합시다. 그 다음 그 분할에 P에 포함되지 않은 x'이라는 임의의 점을 추가한 P'이라는 분할이 있다고 하면 다음 그림과 같이 어떤 구간이 좀 더 잘게 쪼개진 것을 알 수 있습니다. 이때 P'을 분할 P의 세분이라고 합니다.
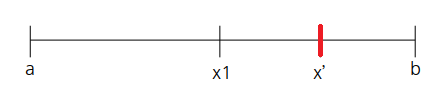
그럼 다음으로 세분할수록 상합은 더 작아지고 하합은 더 커진다는 내용을 자명해 보일 수 있지만 증명해보도록 하겠습니다.(물론 세분하더라도 같은 값일 수 있습니다. ex) 상수 함수)
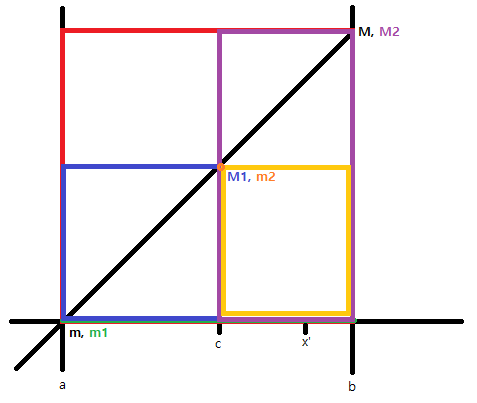
먼저 \(P=\left\{a,b\right\}\)라는 분할이 있다고 해봅시다. 이곳에서 함수 \(f\)의 최댓값을 \(M\), 최솟값을 \(m\)이라고 하겠습니다.
한편 \(P'=\left\{a,c,b\right\}\)라는 세분을 가정해봅시다. 그리고 \([a,c]\)에서의 최대, 최소를 \(M_1,m_1\), \([c,b]\)에서의 최대, 최소를 \(M_2,m_2\)라고 하겠습니다.
그러면 \(M\)은 \([a,b]\)에서 가장 큰 값이고 \(m\)은 가장 작은 값이기 때문에 우리는
(\(M\geq M_1,M_2\)) , (\(m\leq m_1,m_2\))
인 것을 알 수 있습니다.
그러면 (\(M(b-a)\geq M_1(c-a)+M_2(b-c)\)), (\(m(b-a)\leq m_1(c-a)+m_2(b-c)\))라는 당연한 결과를 얻을 수 있습니다.
마찬가지로 P'에서는 c라는 원소가 하나만 있지만, 위의 그림처럼 x'이라는 원소를 넣어 P''같은 세분이 생기면 [c, b]만 놓고 보면 똑같은 결과가 나오는 것을 알 수 있습니다. 결과적으로 P''={a, c, x', b}가 P'보다 상합은 작거나 같고, 하합은 크거나 같은 결과를 얻어 세분할수록 상합은 더 작아지고 하합은 더 커진다는 것을 알 수 있습니다.
상합과 하합의 대소 비교
자, 마지막으로 상합과 하합은 서로 같거나 서로 다른 임의의 분할에 대해 상합이 하합보다 크거나 같다는 증명을 하겠습니다.
먼저 임의의 분할 \(P_1\)과 \(P_2\)가 있다고 해보겠습니다. 그럼 \(U(f,P_1)\)과 \(L(f,P_2)\)의 대소 비교를 해봅시다. 먼저 \(P_1\)과 \(P_2\)를 모두 포함하는 \(P_3\)가 있다고 하겠습니다. 그러면 위의 증명들을 통해 우리는 다음의 결과를 얻게 됩니다. \[U(f,P_1)\leq U(f,P_3) \leq L(f,P_3) \leq L(f,P_2)\]
또한 같은 분할에서는 상합은 넓이의 최댓값을 구한 것이기 때문에 당연히 상합이 클 수밖에 없습니다.
이로써 우리는 아래와 같이 상합이 하합보다 항상 크다는 결과를 얻을 수 있습니다.
\[U(f,P_1)\leq L(f,P_2)\]
이렇게 리만 적분과 좀 더 엄밀한 증명을 해보았는데요. 사실 리만 적분은 정의의 용어가 어렵지 개념 자체는 엄청 어렵지는 않습니다. 그래도 처음 접하고 생소하다 보니 어려우셨을 수도 있었을 텐데요. 여러 번 읽어보면 충분히 무슨 내용인지 이해하실 수 있으실 겁니다.
그럼 오늘 내용은 여기서 마무리하도록 하고 다음 시간에는 마지막으로 연속 함수에서의 리만 적분 가능성과 미적분의 기본정리에 대해 알아볼 텐데요. 다음 시간에는 엡실론-델타 논법에 대한 내용도 다루기 때문에 밑의 포스팅도 같이 읽어보시기를 추천드리겠습니다.
극한의 엄밀한 정의-엡실론 델타 논법(쉽게 다가가보자)
안녕하세요. 오늘은 극한에 대해서 배워보도록 합시다. 미적분에서 극한은 아주 기본이 됩니다. 극한을 기본으로 미적분을 구축해 나가게되죠. 많은 분들이 고등학생때 극한에 대해 배우셨을
gonbuine.tistory.com
'미분적분학' 카테고리의 다른 글
| 미분이란?(미분계수, 미분의 응용) (0) | 2022.12.03 |
|---|---|
| 부정적분과 정적분(고등과정부터 대학과정까지 알아보자)-3 (2) | 2022.11.30 |
| 부정적분과 정적분(고등과정부터 대학과정까지 알아보자.)-1 (0) | 2022.06.19 |
| 극한의 엄밀한 정의-엡실론 델타 논법(쉽게 다가가보자) (0) | 2020.12.21 |
| 삼각함수 덧셈정리 증명 (0) | 2020.11.24 |




댓글